上篇博客我们主要聊了比较高效的归并排序算法,本篇博客我们就来介绍另一种高效的排序算法:快速排序。快速排序的思想与归并排序类似,都是采用分而治之的方式进行排序的。快速排序的思想主要是取出无序序列中第一个值,然后通过比较将比该值小的元素放到该值的前方,将比该值大的元素放在该值的后方。这样一来该值前方的数据都要比该值小,该值后方的数据都要比该值大。然后再次对前半部分和后边半部分无序的数列进行上述操作,这样不断的操作,无序的序列的规模不断被缩小。等问题的规模被缩小到一定程度后,我们的序列就变的有序了。
之前我们说过,当一个问题可以被分成一些相同的子问题时,我们就可以使用递归来操作。所以在快速排序的过程中,我们是通过递归的方式将问题规模逐渐减小,知道序列为序为止。本篇博客将会给出这一过程,根据示意图,给出相应的代码实现。
一、将无序数组进行拆分
在本篇博客,我们先聊一聊如果将大的问题拆分成一些相同的子问题。我们需要对需要排序的数组进行拆分,从无序序列中取出一个值,然后通过比较,将比该值大的放在该值的后方,比该值小的,放在该值的前方。本部分,我们将给出相应的示意图以及代码实现。
1.拆分示意图
下方就是我们上述过程的示意图。也是快速排序第一轮排序的过程。首先将无序数组中的第一个值进行暂存(temp = 62),经过下述步骤,我们会将那些比62小的元素放到62的前面,比62大的元素放到后边。low负责遍历前半部分,将前半部分大于62的值放到后边,而high负责遍历后半部分,将后半部分小于62的值放前边。具体步骤如下所示。

2.代码实现
根据上述示意图,我们可以给出相应的代码实现。如果上述的示意图理解了,看下方代码的实现是比较简单的。partition()函数就负责将一个无序的数组转变的以第一个值为准,较小的值放在该值的前边,较大的放在该值的后边。如下所示。
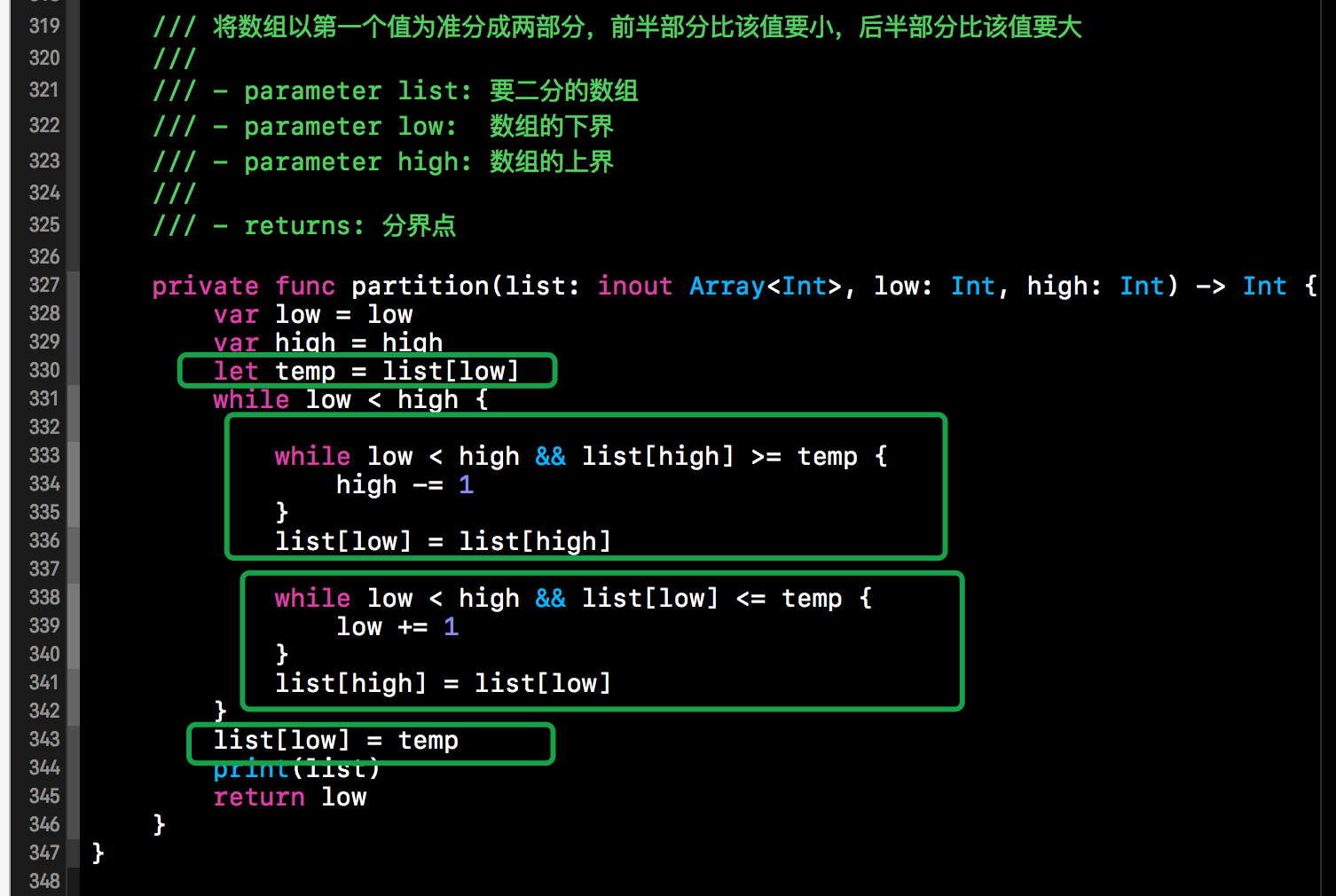
二、快速排序
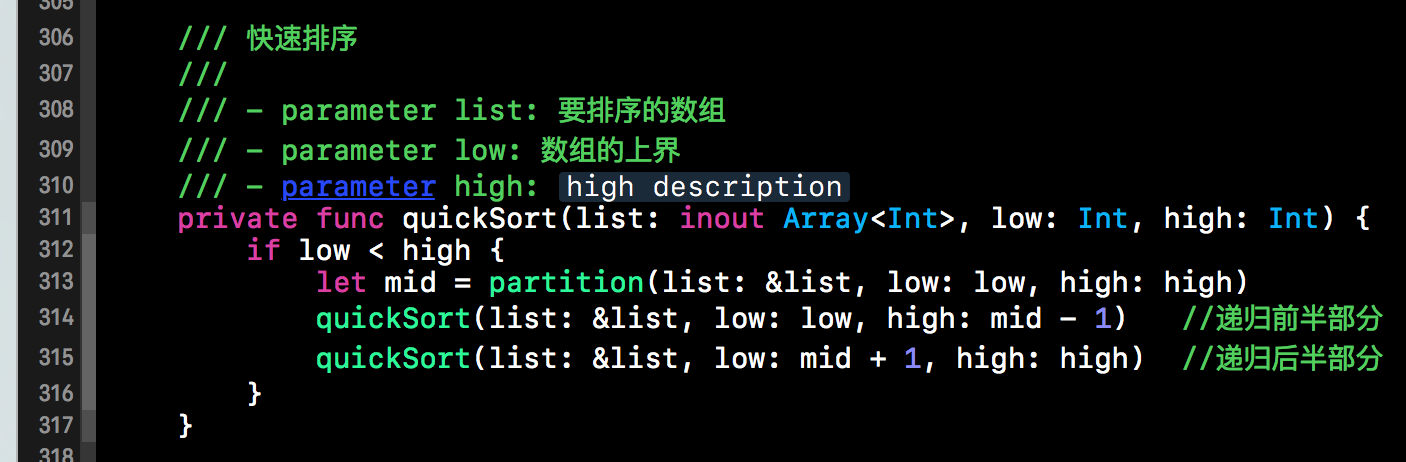
实现完拆分方法后,我们就该实现快速排序的代码了。上面的代码是快排的核心,接下来做的事情是调用上述的函数将无序数组进行拆分,然后再调用上述函数将前后无序的小数组进行拆分,依次执行下去,我们的数组就是有序的了。其实就是一个递归的过程。下方的quickSort()就是这个过程。首先将无需数组调用partition()方法进行拆分,然后再次调用quickSort()方法执行前半部分,同样的调用quickSort()方法执行后半部分。代码如下所示。
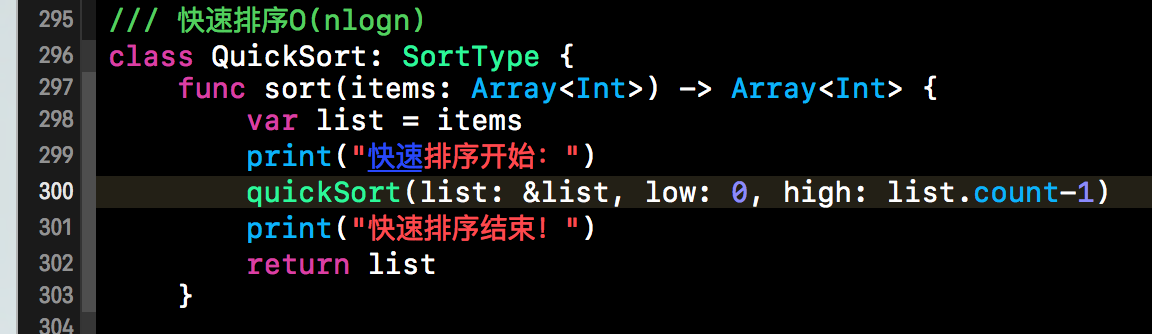
定义完快速排序的核心方法后,接下来就是使用了。下方的QuickSort就是相应的快速排序类,QuickSort还是要遵循SortType这个排序协议的,而sort()方法则是该协议中定义的对外调用的接口。具体代码如下所示。
三、测试用例
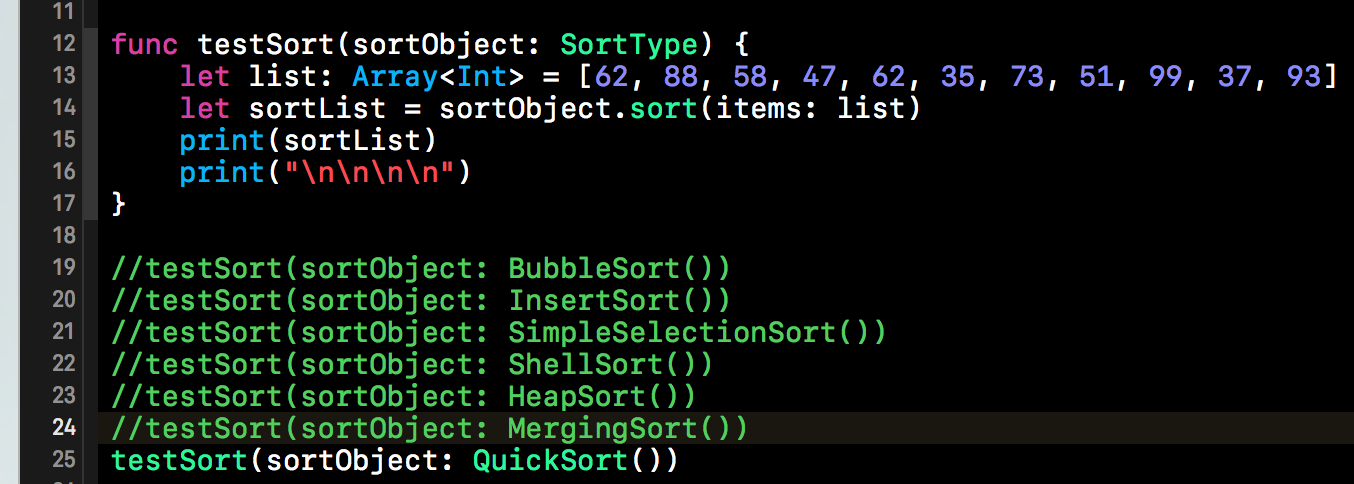
用我QuickSort类遵循了SortType方法,我们依然可以使用之前的测试用例。下方就是我们的测试用例,与之前使用的一直,只不过需要将QuickSort这个类的对象传给我们的测试函数即可,如下所示:
本篇博客快速排序的运行结果如下:
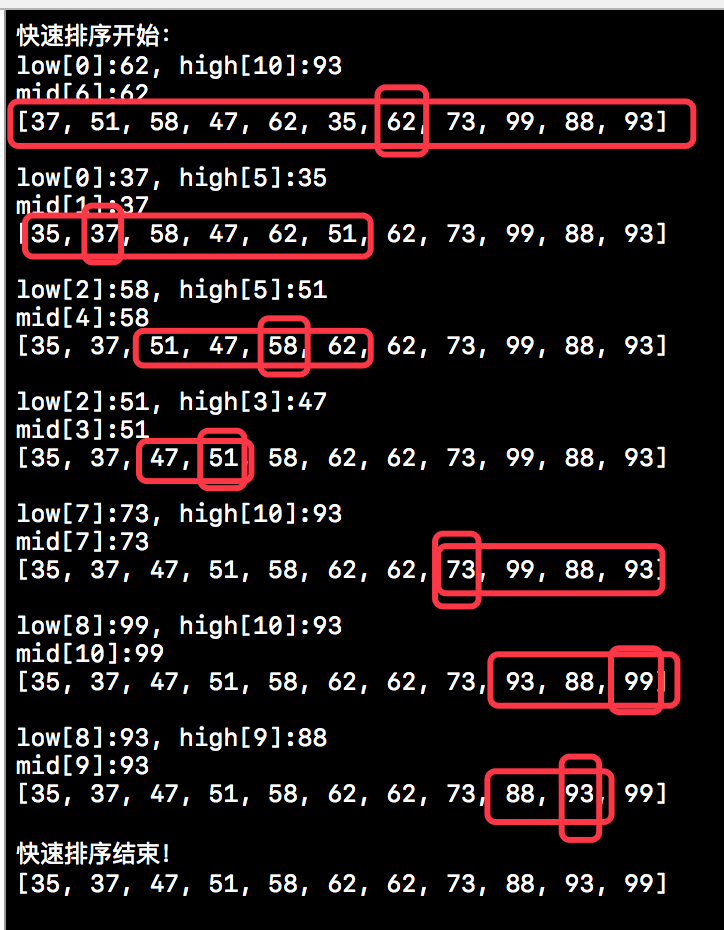
本篇博客对堆排序的介绍就先到这儿,下篇博客我们将会介绍“基数排序”的详细内容。本篇博客的相关代码依然会在github上进行分享,下方是github分享地址,如下所示:
github代码分享地址: